home-icon

Beurteilung der diagn. Aussagekraft einer Laboruntersuchung

Mit welcher Sicherheit können wir erwarten, dass ein Patient, dessen Untersuchungsresultat ausserhalb des Normalbereiches liegt, tatsächlich an der Krankheit X leidet?

Um das zu beurteilen, reicht die Kenntnis von diagnostischer Empfindlichkeit und Spezifität des Untersuchungsverfahrens nicht aus.

Beispiel:

  • Eine Gruppe von 1000 Personen wird untersucht. Die Häufigkeit der Krankheit X beträgt 5%. 50 Personen dieser Gruppe sind demnach krank.
  • Das Untersuchungsverfahren möge folgende Qualität besitzen:
    Empfindlichkeit : 90%
    Spezifität: 90%.

    • Wie sieht das Untersuchungsergebnis aus?

  • Bei einer Empfindlichkeit von 90% werden 9/10 der Kranken richtig durch ein positives Testergebnis erfasst (d.h. in unserem Beispiel 45 Personen).
  • Bei einer Spezifität von 90% werden 9/10 der Nichtkranken richtig durch ein negatives Ergebnis erfasst (d.h. in unserem Beispiel 855 Personen). 95 Nichtkranke zeigen dagegen ein positives Testresultat (Falsch Positive).
  • Insgesamt zeigen 140 Personen der untersuchten Gruppe ein Laborergebnis, das außerhalb des Normalbereiches liegt und damit positiv ist. Unter diesen befinden sich aber nur 45 Kranke. Die Wahrscheinlichkeit für das Vorliegen der Krankheit beträgt also in diesem Fall:

    P = 45 / 140 = 0,32; d.h. 32%.

  • Die Anwendung einer Untersuchung, deren Empfindlichkeit und Spezifität jeweis 90% betragen, bedeutet keinegswegs, dass der Träger eines positiven Ergebnisses mit 90% krank ist. Im gewählten Beispiel sind es nur 32%.
  • Wie hoch diese Wahrscheinlichkeit ist, hängt also nicht nur von den Eigenschaften der Untersuchungsmethode, sondern ebenso davon ab, mit welcher Häufigkeit die zu diagnostizierende Krankheit in der untersuchten Gruppe vorkommt.
    Die Wahrscheinlichkeiten, die angeben, wie häufig bei positivem Laborwert mit der Krankheit, bzw. bei negativem Wert mit dem Fehlen der Krankheit zu rechnen ist, werden als Prädiktive Werte bezeichnet.
    Während Empfindlichkeit und Spezifität Wahrscheinlichkeiten sind, die das Untersuchungsverfahren charakterisieren, gestatten es die Prädiktiven Werte, die diagnostische Aussagekraft zu beurteilen.
    Ihre Berechnung erfolgt mit Hilfe des Theorems von BAYES:
    • Während die Sensitivitä also die Wahrscheinlichkeit ausdrückt. ein posistives Testergebnis (T+) bei einer definitiv vorhandenen Krankheit (K+) zu erhalten
    [ P(T+ | K+) ],

    ist der Prädiktive Wert die Wahrscheinlichkeit, dass bei einem positiven Testergebnis die Krankheit auch vorliegt:
    [ P(K+ | T+) ].

    Die Wahrscheinlichkeit für das gleichzeitige Eintreffen der beiden Ereignisse (symbolisiert mit dem Zeichen "∩") Krankheit vorhanden (K+) und positives Testergebnis (T+) ergibt sich nach dem Multiplikationsgesetz der Wahrscheinlichkeitsrechnung aus der Wahrscheinlichkeit, mit der die Krankheit überhaupt vorhanden ist [ P(K+) ] (= Prävalenz) multipliziert mit der Wahrscheinlichkeit, mit der ein positives Testergebnis bei vorhandener Krankheit dann auch vorliegt:
    P(K+ ∩ T+) = P(K+) P(T+ | K+).

    Gleichbedeutend kann auch gesagt werden, dass die Wahrscheinlichkeit mit der K+ und T+ gleichzeitig auftreten gleich der Wahrscheinlichkeit ist, mit der überhaupt eine positives Testergebnis eintritt multipliziert mit der Wahrscheinlichkeit, mit der dann auch eine Krankheit vorliegt:
    P(K+ ∩ T+) = P(T+) P(K+ | T+).

    Sezt man die beiden letzten Ausdrücke gleich,
    P(K+) P(T+ | K+) = P(T+) P(K+ | T+),

    so erhält man durch Umformen nach P(K+ | T+)einen Ausdruck (Spezielle Bayes-Formel) für die Wahrscheinlichkeit des Vorliegens einer Krankheit bei positivem Testergebnis:
    P(K+) | T+) = P(K+ P(T+ | K+) / P(T+).

    Die totale Wahrscheinlichkeit für das Auftreten eines positiven Ergebnisses überhaupt ergibt sich aus der Summe der Wahrscheinlichkeiten, mit dem das positive Testergebnis bei Kranken und Gesunfen auftritt (Totale Wahrscheinlichkeit):
    P(T+) = P(K+ ∩ T+) + P(K- ∩ T+).
    Die Anwendung des Multiplikationsgesetzes wiederum ergibt
    P(T+) = P(K+) P(T+ | K+) + P(K-) P(T+ | K-).
    Setzt man diesen Ausdruck in die Gleichung für P(K+ | T+) ein und dividiert Zähler und Nenner durch P(K+) P(T+ | K+), so ergibt sich für den Positiven Pädiktiven Wert: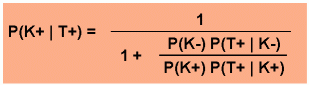

    Darin bedeuten:
    P(T+ | K-): Unspezifiät
    P(T+ | K+): Empfindlichkeit.
    P(K+); P(K-):
  • Das sid die Erwartungswahrscheinlichkeiten für das Vorhandensein bzw. Fehlen der Krankheit X in der untersuchten Gruppe.
  • Sie sind unabhängig von der geplanten Untersuchung und bilden eine der Voraussetzungen für deren Einsatz. Man nennt sie A-priori-Wahrscheinlichkeiten.
  • Für den Fall einer Screening-Untersuchung sind die Erwartungswahrscheinlichkeiten gleich der Krankheitsprävalenz.
  • Für die klinische Diagnostik interessiert uns nicht die Krankheitsprävalenz in der Gesamtbevölkerung, sondern die entsprechende Häufigkeit in der zu untersuchenden Gruppe.

    • Bei einer angenommenen Spezifität und Sensitivität von 95% und wächst der Positive Vorhersagewert von 8,7% über 50% auf 95% mit Steigerung der Prävalenz von 0,5% über 5% auf 50%, z.B. durch vorherige körperliche Untersuchung.

    Der Negative Prädiktive Wert gibt die Wahrscheinlichkeit an, mit der der Träger eines normalen Laborwertes tatsächlich frei von der auszuschließenden Krankheit ist:
    P(K- | T-).

    Im Übrigen gilt auch hier das bereits zum positiven Prädiktiven Wert ausgeführte, nur eben auf den Zustand "Nichtkrank" bezogen.

    Berechnung: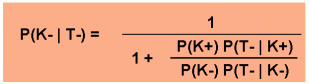